gridpack::math::NewtonRaphsonSolverImplementation< T, I > Class Template Reference

Implementation of Newton-Raphson method to solve a system of nonlinear equations in parallel. More...

#include <newton_raphson_solver_implementation.hpp>

Inheritance diagram for gridpack::math::NewtonRaphsonSolverImplementation< T, I >:

[legend]

Collaboration diagram for gridpack::math::NewtonRaphsonSolverImplementation< T, I >:

[legend]

List of all members.

Public Types
typedef NonlinearSolverImplementation < T, I >::VectorType	VectorType
typedef NonlinearSolverImplementation < T, I >::JacobianBuilder	JacobianBuilder
typedef NonlinearSolverImplementation < T, I >::FunctionBuilder	FunctionBuilder
Public Member Functions
	NewtonRaphsonSolverImplementation (const parallel::Communicator &comm, const int &local_size, JacobianBuilder form_jacobian, FunctionBuilder form_function)
	Default constructor.
	NewtonRaphsonSolverImplementation (MatrixT< T, I > &J, JacobianBuilder form_jacobian, FunctionBuilder form_function)
	Construct with an existing Jacobian Matrix.
	~NewtonRaphsonSolverImplementation (void)
	Destructor.

Detailed Description

template<typename T, typename I>
class gridpack::math::NewtonRaphsonSolverImplementation< T, I >

Implementation of Newton-Raphson method to solve a system of nonlinear equations in parallel.

This class implements the Newton-Raphson method to solve a system of nonlinear equations in the form

$\left[ \mathbf{J}\left( \mathbf{x} \right) \right] \Delta \mathbf{x} ~ = ~ -\mathbf{F}\left( \mathbf{x} \right)$

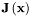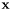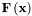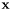where $\mathbf{J}\left( \mathbf{x} \right)$ is the Jacobian matrix, $\mathbf{x}$ is the solution Vector, and $\mathbf{F}\left( \mathbf{x} \right)$ is some Vector function of $\mathbf{x}$ .

Each successive solution estimate is computed as

$\mathbf{x}^{k+1} ~ = \mathbf{x}^{k} + \Delta \mathbf{x}^{k}$

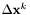where $\Delta \mathbf{x}^{k}$ is determined by solving the linear system

$\left[ \mathbf{J} \left( \mathbf{x}^{k} \right) \right] \Delta \mathbf{x}^{k} ~ = ~ -\mathbf{F}\left( \mathbf{x}^{k} \right)$

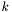and $ k $ is the number of the previous iteration.

The interative process is ended when the L² norm of 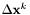$\Delta \mathbf{x}^{k}$ is less then some specified small tolerance.

Member Typedef Documentation

template<typename T , typename I >

typedef NonlinearSolverImplementation<T, I>::FunctionBuilder gridpack::math::NewtonRaphsonSolverImplementation< T, I >::FunctionBuilder

Reimplemented from gridpack::math::NonlinearSolverImplementation< T, I >.

template<typename T , typename I >

typedef NonlinearSolverImplementation<T, I>::JacobianBuilder gridpack::math::NewtonRaphsonSolverImplementation< T, I >::JacobianBuilder

Reimplemented from gridpack::math::NonlinearSolverImplementation< T, I >.

template<typename T , typename I >

typedef NonlinearSolverImplementation<T, I>::VectorType gridpack::math::NewtonRaphsonSolverImplementation< T, I >::VectorType

Reimplemented from gridpack::math::NonlinearSolverImplementation< T, I >.

Constructor & Destructor Documentation

template<typename T , typename I >

gridpack::math::NewtonRaphsonSolverImplementation< T, I >::NewtonRaphsonSolverImplementation	(	const parallel::Communicator &	comm,
		const int &	local_size,
		JacobianBuilder	form_jacobian,
		FunctionBuilder	form_function
	)

Default constructor.

Collective.

A NonlinearSolverImplementation must be constructed simultaneously on all processes involved in comm.

Parameters:

	comm	communicator on which the instance is to exist
	local_size	number Jacobian rows and Vector entries to be owned by this process
	form_jacobian	function to fill the Jacobian Matrix, $\left[ \mathbf{J}\left( \mathbf{x} \right) \right]$
	form_function	function to fill the RHS function Vector, 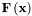$\mathbf{F}\left( \mathbf{x} \right)$

Returns:: new NonlinearSolverImplementation instance

References gridpack::utility::Configurable::configurationKey().

template<typename T , typename I >

gridpack::math::NewtonRaphsonSolverImplementation< T, I >::NewtonRaphsonSolverImplementation	(	MatrixT< T, I > &	J,
		JacobianBuilder	form_jacobian,
		FunctionBuilder	form_function
	)

Construct with an existing Jacobian Matrix.

References gridpack::utility::Configurable::configurationKey().

template<typename T , typename I >

gridpack::math::NewtonRaphsonSolverImplementation< T, I >::~NewtonRaphsonSolverImplementation ( void )

Destructor.

This must be called simultaneously by all processes involved in the communicator used for construction.

The documentation for this class was generated from the following file:

newton_raphson_solver_implementation.hpp

gridpack::math::NewtonRaphsonSolverImplementation< T, I > Class Template Reference

Public Types

Public Member Functions

Detailed Description

template<typename T, typename I> class gridpack::math::NewtonRaphsonSolverImplementation< T, I >

Member Typedef Documentation

Constructor & Destructor Documentation

template<typename T, typename I>
class gridpack::math::NewtonRaphsonSolverImplementation< T, I >